Ch4.差分隐私

• 差分隐私与 k-匿名性的区别

  • k-匿名性是数据的性质.
    差分隐私是算法的性质.
  • 验证 k-匿名性是验证数据集是否满足.
    验证差分隐私是验证产生数据集的算法是否满足.

• 临近数据集 (Neighboring Dataset)

  两个数据集中只有一个个体的数据项不同.

• 机制 Mechanism

  满足差分隐私的函数.

  对于所有临近数据集 $x$ 和 $x'$ 和所有可能是输出 $S$, 机制 $F$ 均满足:

  $$\frac{Pr[F(x) = S]}{Pr[F(x') = S]} \leq e^{\epsilon}$$

  则称机制 $F$ 满足差分隐私.

  $F$ 是一个随机函数. 相同的输入, 可能会有多个输出.

  $F$ 要达到的效果是: 输入 $x$ 和 $x'$ 到 $F$, 攻击者无法分辨 $F$ 给出的输出是属于 $x$, 还是属于 $x'$.

• 隐私参数 (Privacy Parameter) / 隐私预算 (Privacy Budget) $\epsilon$

  • $\epsilon$ 越小, $F$ 给出的输出越相似, 也就能提供更好的隐私性.
  • $\epsilon$ 取值共识:
    • $\epsilon \approx 1 \ || \ \epsilon < 1$
    • $\epsilon > 10$ 则大概率无法提供足够的隐私性.

      以上取值经验过于保守.

4.1 拉普拉斯机制

• 满足差分隐私的最简单方法: 查询结果添加随机噪声.

  eg. 查询一个班级的数学平均成绩.
  真实平均成绩: 89.0
  查询输出成绩: 87.1 / 90.2 / …

• 拉普拉斯机制 (Laplace Mechanism)

  最典型的基础机制.

  $$F(x) = f(x) + Lap(\frac{s}{\epsilon})$$
  • $Lap(S)$ 是以均值为 0, 缩放系数为 $S$ 的拉普拉斯分布采样.
  • $s$ 是 $f$ 的敏感度 (Sensitivity).

    $x$ 变为 $x'$ 后, $f$ 输出的变化量.

  • 计数问询 (Counting Query)

    满足某些特定条件的数据项有多少.

  import numpy as np
  
  # 差分隐私机制(查询返回值添加随机噪声)
  def differentially_private_mean(data, sensitivity, epsilon):
    true_mean = np.mean(data)
    noise = np.random.laplace(0,  sensitivity　/ epsilon)
    return true_mean + noise
  
  # 数据集
  dataset = np.array([30, 40, 50, 60, 70])
  
  # 隐私预算
  epsilon = 0.1
  # 敏感度
  sensitivity = 1.0
  
  # 差分隐私查询
  private_result = differentially_private_mean(database, sensitivity, epsilon)
  print(f"差分隐私查询结果: {private_result}")
  

  虽然查询输出的不是真实的数据, 但斗都与真实值很接近, 仍有较高的可用性.

4.2 需要多大的噪声?

下面的代码比较了不同隐私预算下的查询结果

import numpy as np

# 差分隐私机制(查询返回值添加随机噪声)
def differentially_private_mean(data, sensitivity, epsilon):
    true_mean = np.mean(data)
    noise = np.random.laplace(0, sensitivity / epsilon)
    return true_mean + noise

# 数据集
dataset = np.array([30, 40, 50, 60, 70])

# 实际均值
true_mean = np.mean(dataset)
print(f"真实均值: {true_mean} \n")

# 设置不同的隐私预算 epsilon 值
epsilon_values = [0.01, 0.1, 1.0, 10.0]
sensitivity = 1.0
num_trials = 5  # 进行多次实验

for _ in range(num_trials):
    for epsilon in epsilon_values:
        private_result = differentially_private_mean(dataset, sensitivity, epsilon)
        print(f"{epsilon}: {float(round(private_result, 4))}")
    print('\n')

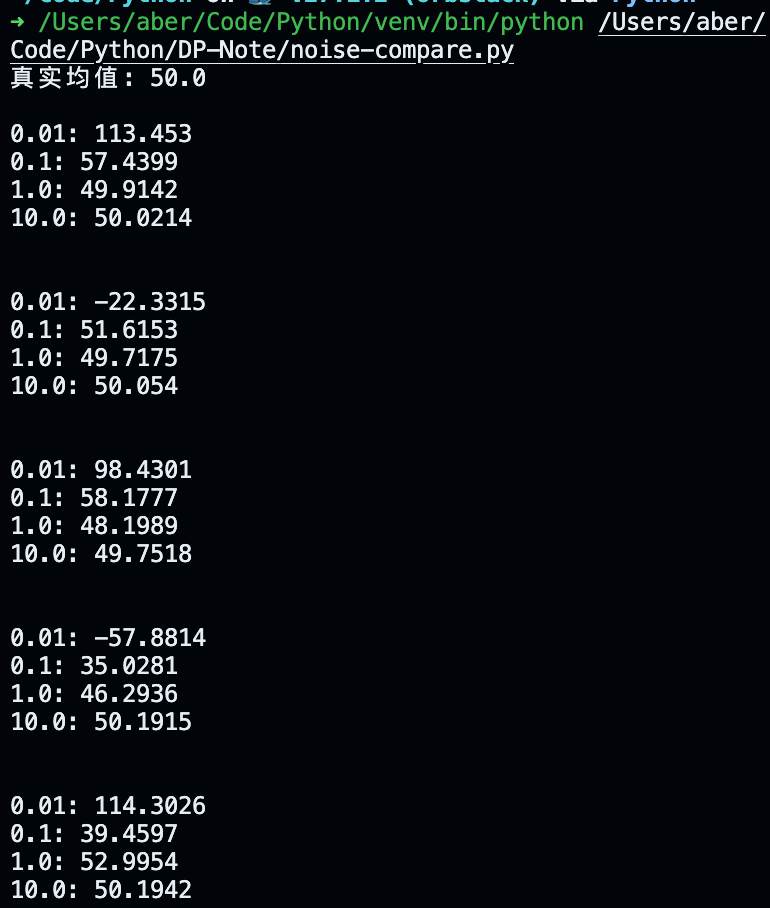
进行多次查询, 结果可以看出: 隐私预算越小, 与真实值差距越大. 隐私预算越大, 也就越接近真实值.