Ch5.差分隐私的性质

5.1 串行组合性

串行组合性 Sequential Composition

$F_1(x)$ 满足 $\epsilon_1$-差分隐私
$F_2(x)$ 满足 $\epsilon_2$-差分隐私
$G(x)=(F_1(x),F_2(x))$, 则满足 $\epsilon_1 + \epsilon_2$-差分隐私

串行组合性得到的是隐私消耗的上界, 实际消耗量应小于串行组合性估计的消耗量.

epsilon1 = 1 
epsilon2 = 1 
epsilon_total = 2  
# 满足 1-差分隐私 
def F1(): 
  return np.random.laplace(loc=0, scale=1/epsilon1)  
# 满足 1-差分隐私 
def F2():
  return np.random.laplace(loc=0, scale=1/epsilon2) 
# 满足 2-差分隐私 
def F3(): 
  return np.random.laplace(loc=0, scale=1/epsilon_total)  

# 根据串行组合性, 满足 2-差分隐私 
def F_combined(): 
  return (F1() + F2()) / 2

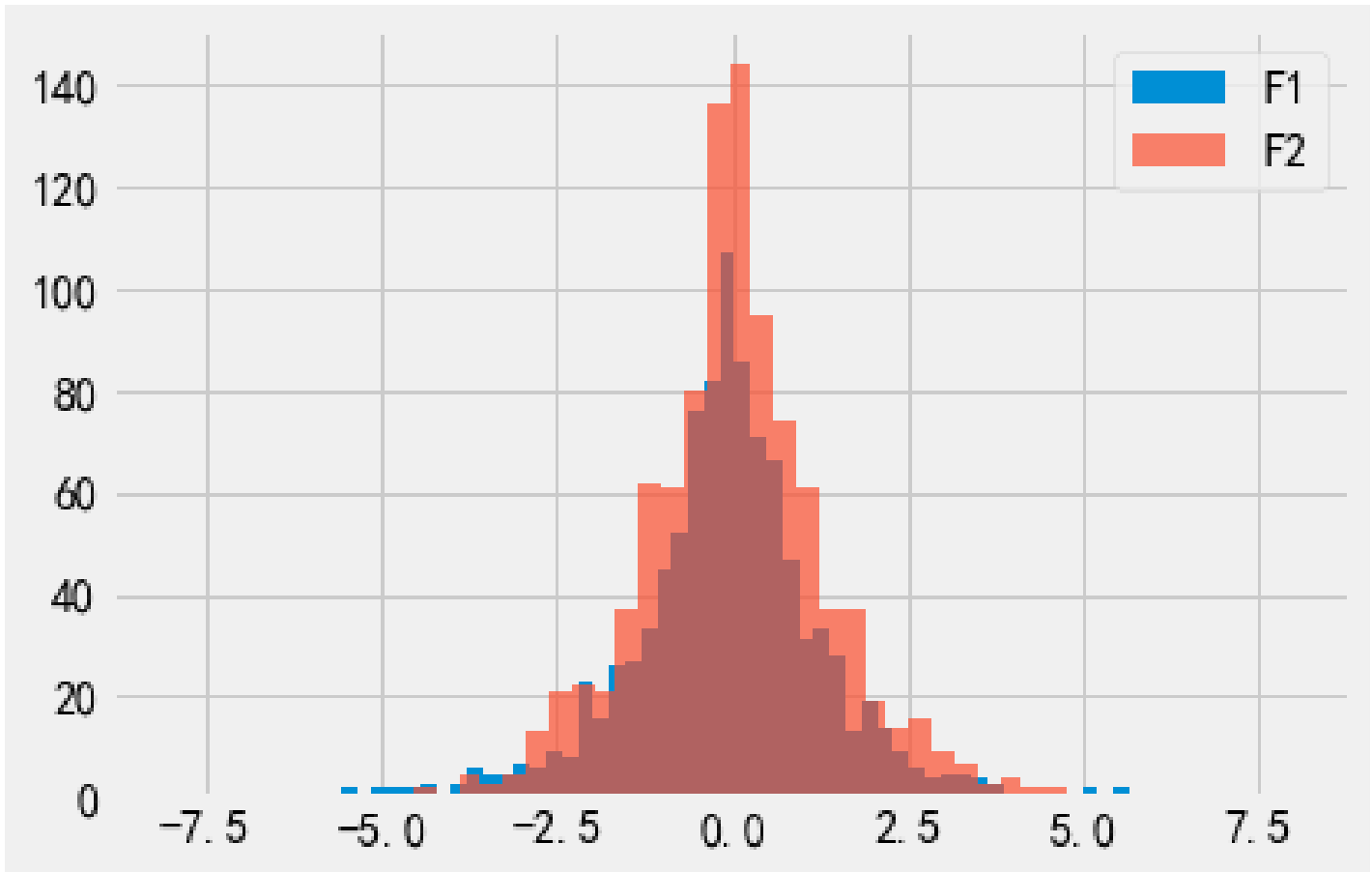
F1 与 F2 的隐私预算相同, 都为 1, 所以输出的分布也相似.

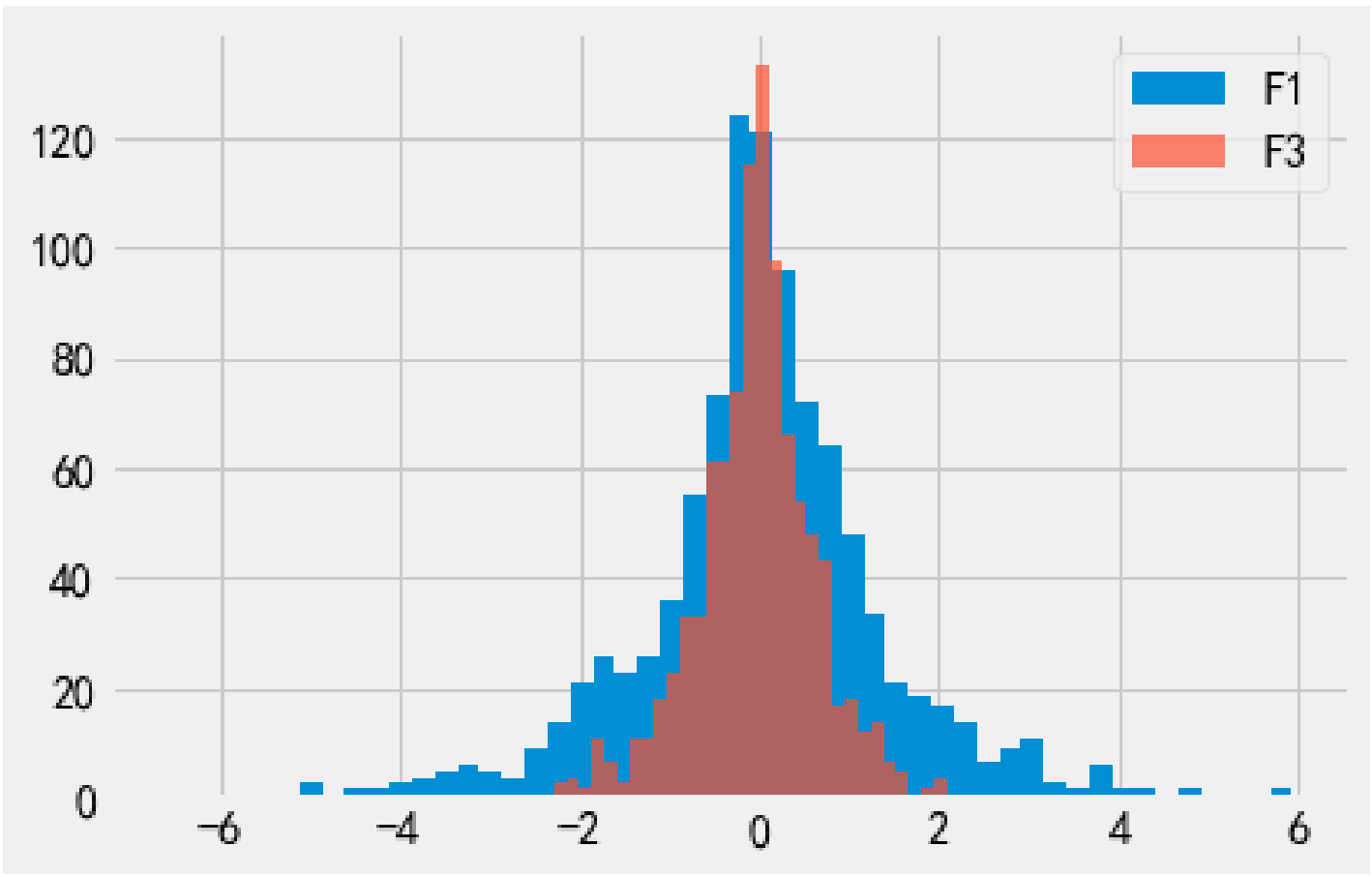
F3 和 F_combined 的隐私预算都大于 F1 的隐私预算, 输出也就更接近真实值, F3 和 F_combined 的隐私性 也就要弱于 F1.

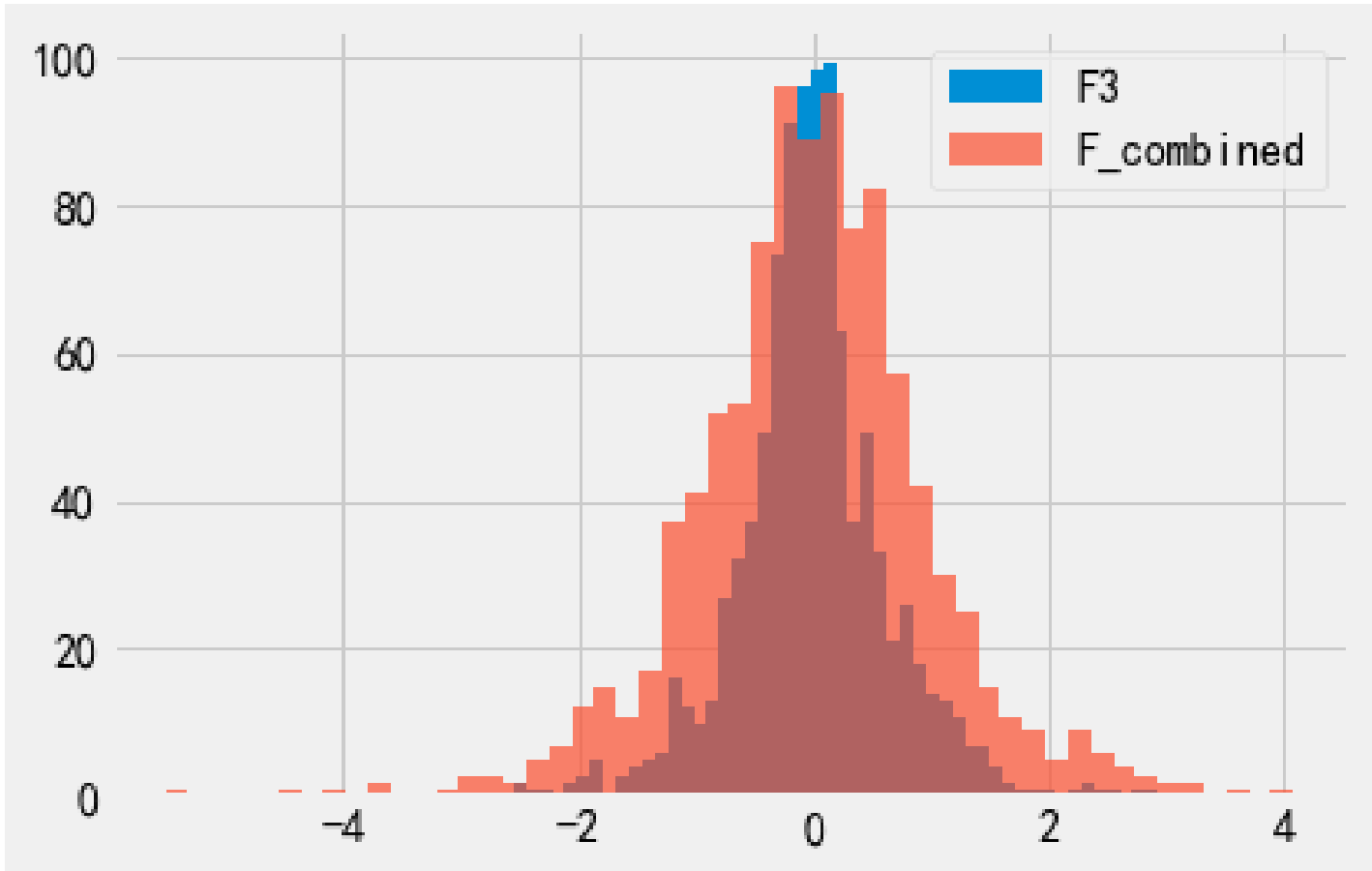
F_combined 的隐私预算通过串行组合性计算为 1+1=2. 虽然 F3 和 F_combined 的隐私预算都为 2, 但 F_combined 的实际隐私消耗量会小于估计的, 所以 F_combined 的实际隐私消耗其实是小于 F3 的, 隐私性也就比 F3 更好.

5.2 并行组合性

并行组合性 Parallel Composition

• 将数据集拆分为互不相交的子数据块, 再在子数据块上应用差分隐私机制.

  子数据块互不相交, 每个个体也就仅会存在与一个块中.

若 $F(x)$ 满足 $\epsilon$-差分隐私, 将数据集 $X$ 切分为 k 个互不相交的子数据块 $x_1 \cup \dots \cup x_k = X$, 则发布的所有结果 $F(x_1),\dots,F(x_k)$ 的机制满足 $\epsilon$-差分隐私.

运行 k 次 F, 串行组合性计算的隐私消耗为 $k\epsilon$, 而并行组合性计算的隐私消耗仅为 $\epsilon$.

在并行组合性中, 数据集中的每个个体仅出现一次, 隐私消耗为 $\epsilon$.
在串行组合性中, 每个个体一共出现了 k 次, 每次都会消耗 $\epsilon$. 所以最终每个个体的隐私消耗量为 $k\epsilon$.

5.2.1 直方图

直方图 (Histogram) 按属性将数据分到各个”桶”(子数据块)中. 属性值是互斥的, 用户只会存在于一个”桶”中.

5.2.2 列联表

列联表 (Contingency Table) / 交叉列表 (Cross Tabulation) / 交叉表 (Crosstab), 相当于高维的直方图. 将直方图的”桶”再按另一个属性进行拆分.

如果使用更多属性对数据集进行拆分, 计数值会逐渐变小. 在添加噪声时, 噪声对较大的计数值的可用性没有太大影响, 但噪声可能会把较小的计数值淹没, 导致较小的计数值没有可用性.

5.3 后处理性

后处理性 (Post-processing)

不可能通过某种方式对差分隐私保护下的数据进行后处理, 来降低差分隐私的隐私保护程度.

如果 F(X) 满足 $\epsilon$-差分隐私, 则对任意(确定/随机)函数 g(F(X)) 也满足 $\epsilon$-差分隐私.

??? 使用满足差分隐私的输出数据, 再怎么处理也无法获得额外更接近真实值的数据.