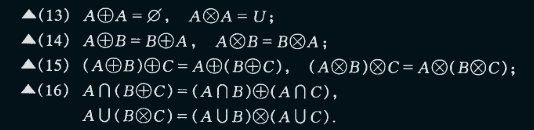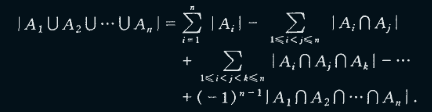aBER 🔬
Back to note
•
5 min read

Discrete Mathematics Review

Table of Contents

第一章 命题逻辑

1.1 命题符号化

  • 命题
    • 具有唯一真/假值的陈述句
  • 简单命题
    • 一个命题是一个简单陈述句
  • 复杂命题
    • 简单命题通过命题联结词组成的命题
  • 命题联结词
    • image.png
      • 否定词 ¬\neg
      • 合取词 ∧\wedge
      • 析取词 ∨\vee
      • 蕴含词 →\rightarrow
      • 等值词 ↔\leftrightarrow
  • 条件命题
    • P→QP \rightarrow Q
  • 双条件命题
    • P↔QP \leftrightarrow Q
  • 命题变元
    • P 既可以表示真命题，也可以表示假命题
  • 命题常元
    • T 永远表示真命题
    • F 永远表示假命题

1.2 合式公式

  • 合式公式
    • 命题常元/命题变元
    • 合式公式组成的复杂命题
    • 有限次的使用以上两项得到的符号串
  • 子公式
    • 是合式公式的一部分且本身也是合式公式
  • 真子公式
    • 不同于自身的子公式
  • 代入实例
    • 用一个合式公式中的变元替换另一个合式公式中所有对应的变元
  • 代入
    • 将被取代的命题变元的所有出现的地方都进行取代，并且是同时进行取代
    • 对于命题变元而言
  • 替换
    • 将被取代的子公式的一处或几处进行替换，不需要替换所有

1.3 永真公式

  • 命题公式的解释
    • 一组合式公式中命题变元的真值赋值
    • 记作 I=P1∼P2∼…Pn∼I=\overset{\sim}{P_1}\overset{\sim}{P_2}\dots\overset{\sim}{P_n}
      • Pi∼=1 or 0\overset{\sim}{P_i} = 1 \ or \ 0
  • 合式公式分类
    • 永真式（重言式）
      • 任何解释下都为真
    • 永假式（矛盾式）
      • 任何解释下都为假
    • 可满足式
      • 至少有一个解释使得为真
  • 逻辑恒等式
    • image.png
    • A↔BA \leftrightarrow B 为永真式，A 恒等于 B，A 等价于 B，记为 A⇔BA \Leftrightarrow B
    • 性质
      • A⇔AA \Leftrightarrow A
      • A⇔B,B⇔AA \Leftrightarrow B, B \Leftrightarrow A
      • A⇔B且B⇔C，A⇔BA \Leftrightarrow B 且 B \Leftrightarrow C，A \Leftrightarrow B
      • A⇔B,¬A⇔¬BA \Leftrightarrow B,\neg A \Leftrightarrow \neg B
  • 对偶式
    • 将仅含 ¬,∧,∨\neg,\wedge,\vee 的合式公式的 ∧\wedge 和 ∨\vee 互换，T 和 F 互换
    • 记为 A∗A^*
  • 永真蕴含式
    • image.png
    • A→BA \rightarrow B 为永真式，记为 A⇒BA \Rightarrow B
    • 性质
      • A⇒AA \Rightarrow A
      • A⇒B,B⇒AA \Rightarrow B, B \Rightarrow A
      • A⇔B当且仅当A⇒B且B⇒AA \Leftrightarrow B 当且仅当 A \Rightarrow B且B \Rightarrow A
      • A⇒B,¬B⇒¬AA \Rightarrow B,\neg B \Rightarrow \neg A
  • 定理
    • 1.3.1 代入规则
      • 永真式的代入实例是永真式
    • 1.3.2 替换规则
      • 设 A 是 C 的子公式，且 A⇔BA \Leftrightarrow B，若用 B 替换 C 中的 A 的一处或多处出现得到合式公式 D，则 C⇔DC \Leftrightarrow D
    • 1.3.3
      • 设 A(P1,P2,…,Pn)A(P_1,P_2,\dots,P_n) 是仅含 ¬,∧,∨\neg,\wedge,\vee 的公式，则 ¬A(P1,P2,…,Pn)⇔¬A∗(¬P1,¬P2,…,¬Pn)\neg A(P_1,P_2,\dots,P_n) \Leftrightarrow \neg A^*( \neg P_1,\neg P_2,\dots,\neg P_n)
    • 1.3.4 对偶定理
      • 设 A 和 B 是仅含 ¬,∧,∨\neg,\wedge,\vee 的合式公式，若 A⇔BA \Leftrightarrow B，则 A∗⇔B∗A^* \Leftrightarrow B^*
    • 1.3.5
      • 设 A 和 B 是仅含 ¬,∧,∨\neg,\wedge,\vee 的合式公式，若 A⇒BA \Rightarrow B，则 B∗⇒A∗B^* \Rightarrow A^*

1.4 范式

  • 文字
    • 正文字
      • 命题变元
    • 负文字
      • 命题变元的否定
  • 基本和
    • 文字
    • 基本和的析取 ∨\vee
  • 合取范式
    • 基本和
    • 合取范式的合取 ∧\wedge
    • 求法
      • 消去 →\rightarrow 和 ↔\leftrightarrow
      • 消去双重否定
      • 使用分配律、结合律等进行变化
  • 极大项
    • 所有变元的析取 M=P1b1∨P2b2∨⋯∨PnbnM = P_1^{b_1} \vee P_2^{b_2} \vee \dots \vee P_n^{b_n}, b 取 1 或 0
    • 极大项有且仅有一个解释使其为假
  • 主合取范式
    • 极大项
    • 主合取范式的合取 ∧\wedge
    • 求法
      • 先求合取范式
      • 去掉永真的合取范式的基本和
      • 合并相同的文字和基本和
      • 对基本和中补入未出现的命题变元，展开并化简
  • 基本积
    • 文字
    • 文字的合取 ∧\wedge
  • 析取范式
    • 基本积
    • 析取范式的析取 ∧\wedge
  • 极小项
    • 所有变元的析取 m=P1b1∧P2b2∧⋯∧Pnbnm = P_1^{b_1} \wedge P_2^{b_2} \wedge \dots \wedge P_n^{b_n}, b 取 1 或 0
    • 极小项有且仅有一个解释使其为真
  • 主析取范式
    • 极小项
    • 主析取范式的析取 ∧\wedge

第二章 一阶逻辑

2.1 命题符号化

  • 个体
    • 讨论对象
  • 个体词
    • 表示个体的符号
  • 个体常元
    • 一个个体词表示一个特定个体，常用 a，b，c 来表示
  • 个体变元
    • 一个个体词泛指任何一个个体
  • 个体域/论域
    • 个体变元的取值范围
  • 量词
    • 全称量词 ∀\forall
      • 所有，任意，一切
    • 存在量词 ∃\exists
      • 存在，有些，至少存在一个
  • 全总个体域
    • 个体域是一切事物的集合
  • 特性谓词
    • 限制个体变元取值范围的词

2.2 合式公式

  • 项
    • 个体常元和个体变元
    • 项的函数
    • 有限次使用以上两项得到的符号串
  • 原子公式
    • t1,t2,…,tnt_1,t_2,\dots,t_n 是项，P(n)(t1,t2,…,tn)P^{(n)}(t_1,t_2,\dots,t_n) 是原子公式
  • 合式公式
    • 原子公式
    • 合式公式之间的，¬,∧,∨,→,↔,∀,∃\neg,\wedge,\vee,\rightarrow,\leftrightarrow,\forall,\exists
    • 有限次使用以上两项
  • 辖域
    • ∀\forall 或 ∃\exists 限制变元
    • 约束出现
      • 约束变元
        • 在辖域中出现的变元
    • 自由出现
      • 自由变元
      • 非约束出现的变元

2.3 永真公式

  • 永真式
    • 任何解释下都为真
  • 永假式
    • 任何解释下都为假
  • 可满足式
    • 至少有一个解释为真

2.4 范式

  • 前束范式
    • 量词全在公式前
    • 求法
      • 消去 →\rightarrow 和 ↔\leftrightarrow
      • 消去双重否定，将 ¬\neg 移到公式前面
      • 有必要可换名
      • 基本永真式将量词移到最左边
  • 前束词
    • 公式前的所有约束词
  • 母式
  • Skolem 变换
    • 将 ∃\exists 去掉
    • 用新的函数来替换变元
  • Skolem 范式
    • 由 Skolem 得到的范式

2.5 推理理论

  • 全称指定规则 US
    • ∀xA(x)⇒A(y)\forall x A(x) \Rightarrow A(y)
  • 存在推广规则 EG
    • A(c)⇒∃xA(x)A(c) \Rightarrow \exists x A(x)
  • 存在指定规则 ES
    • ∃xA(x)⇒A(c)\exists x A(x) \Rightarrow A (c)
  • 全称推广规则 UG
    • A(y)⇒∀xA(x)A(y) \Rightarrow \forall x A(x)

第三章 集合

3.1 集合的基本概念&表示法

  • 集合
    • 自然数集 NN
    • 整数集 II
      • 正整数 I+I_+
      • 负整数 I−I_-
    • 有理数集 QQ
      • 正有理数 Q+Q_+
      • 负有理数 Q−Q_-
    • 实数集 RR
      • 正实数 R+R_+
      • 负实数 R−R_-
    • 复数集 CC
  • 空集 ∅\emptyset
  • 非空集
  • 有限集
  • 无限集
  • 集合表示法
    • 列举法
      • {1,2,3,4,… }\{1,2,3,4,\dots\}
    • 描述法
      • A={x∣x∈N∧x≥1∧x≤5}A=\{x|x \in N \wedge x \geq 1 \wedge x \leq 5 \}
    • 归纳定义法
      • 基本步
      • 归纳步
      • 极小化

3.2 集合的运算

  • 并
  • 交
  • 差
  • 补
    • A 与 B 不相交
    • 相对补
      • 相对于集合之间
      • A−BA - B
    • 绝对补
      • 相对于全集
      • A‾\overline{A}
  • 集类
    • 以集合为元素
  • 广义交
    • 所有集合共有的元素
  • 广义并
    • 任何集合中出现过的元素
  • 环和
    • A⊕B=(A−B)∪(B−A)A \oplus B = (A - B) \cup (B - A)
  • 环积
    • A⊗B=A⊕B‾A \otimes B = \overline{A \oplus B}
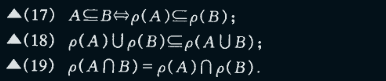
  • 幂集
    • 所有子集组成的集合

3.3 集合恒等式

  • 集合恒等式
    • image.png|353image.png|409image.png|467image.png
  • 容斥原理
    • image.png

3.5 集合的笛卡尔积

  • 笛卡尔积
    • A1×A2×…×An={<a1,a2,…,an>∣ai∈Ai,i=1,2,…,n}A_1 \times A_2 \times \ldots \times A_n = \{<a_1, a_2, \ldots, a_n> \mid a_i \in A_i, i = 1, 2, \ldots, n\}

第四章 二元关系

4.1 关系&表示法

4.2 关系的性质

4.3 关系的运算

4.4 等价关系与划分

4.5 序关系

第五章 函数

5.1 函数的基本概念和性质

5.2 函数的合成

5.3 逆函数

第六章 集合的基数

6.1 可数集和不可数集

6.2 集合基数的比较

第七章 代数系统

7.1 代数运算与代数系统

7.2 动态与同构

第八章 半群和群

8.4 循环群和变换群

第九章 环和域

9.3 多项式环

9.4 有限域

第十一章 图

11.1 图的基本概念

11.2 通路、环路和连通性

11.3 图的矩阵表示

11.4 欧拉图和哈密尔顿图

11.7 树