Content Security Review

第一章 概论

• 定义
  • 内容的获取、识别和管控/分析
• 内涵
  • 法律合法
  • 政治健康
  • 道德规范
• 安全威胁
  • 国家安全
  • 公共安全
  • 文化安全
• 三分类模型
  • 
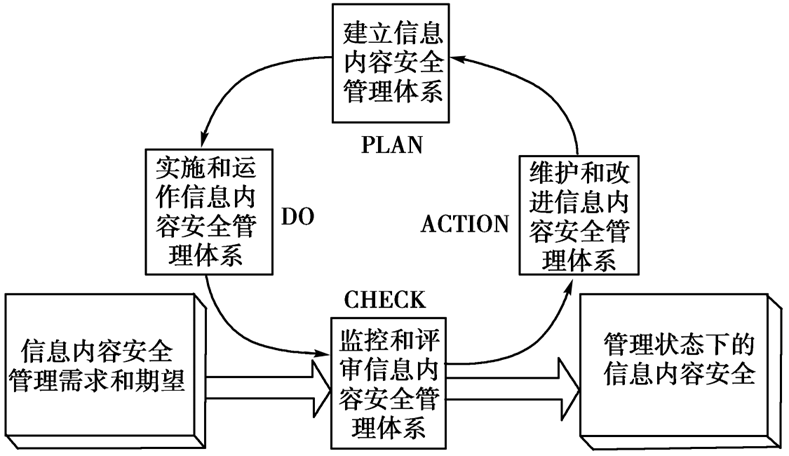
• 戴明环管理框架
  • PDCA
  • 

第二章 内容获取技术

PageRank 算法

• 信息检索 - 搜索引擎
• PageRank 值越高，网页越重要。
• 基本定义
  • 转移矩阵 $M$（结点间的跳转概率矩阵）
  • 初始分布向量 $R_0$ （等概率 $\frac{1}{n}$）
  • $MR = R$
• 一般定义
  • 在基本定义上增加平滑项（避免 0 概率）
  • $R = dMR + \frac{1-d}{n} \boldsymbol{1}$
    • $d$ 为阻尼因子，$0 \leq d \leq 1$, 通常取 0.85
      • 接近 1，随机游走主要依照 $M$ 进行
      • 接近 0, 随机游走等概率随机访问各结点
• 迭代计算
  • $R_{t+1} = dMR_t + \frac{1-d}{n} \boldsymbol{1}$
  • $R_{t+1}$ 与 $R_t$ 充分接近则停止
• 计算过程
  • 转移矩阵 $M$
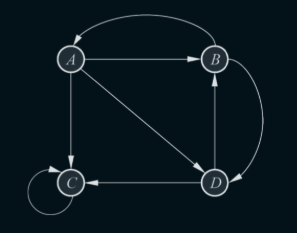
    • 有向图
      • 
    • 转移矩阵
      • 
    • dM
      • 阻尼因子 $d$ = 0.8
      • 
  • 初始分布向量 $R_0$ （等概率 $\frac{1}{n}$）
  • $\frac{1-d}{n} \boldsymbol{1} = \begin{bmatrix} \frac{1}{20} \\ \frac{1}{20} \\ \frac{1}{20} \\ \frac{1}{20} \end{bmatrix}$
  • 最后进行迭代计算
    • 迭代公式 $R_{t+1} = dMR_t + \frac{1-d}{n} \boldsymbol{1}$
    • 
  • 

协同过滤推荐

• 信息推荐算法
• 通过找到与当前用户相似的其他用户，来加权计算最适合当前用户的商品
• $v_{ij}^* = v_i + K \sum_{v_{kj \ne ?}} u_{ik}(v_{kj} - v_k)$
  • $v_{ki \ne ?}$ 表示求和中仅计算用户已评分的商品
  • 用户 $i$ 与用户 $k$ 相似度 $sim(u,v) = u_{ik} = \frac{\sum (v_{ij} - v_i)(v_{kj} - v_k)}{\sqrt{\sum_j(v_{ij} - v_i)^2 \sum_j(v_{kj} - v_k)^2}}$
    • $v_{ij}$ 表示用户 $i$ 对商品 $j$ 的评分
    • $v_i$ 表示用户 $i$ 已评分商品的平均分
  • $K$ 为当前用户 $i$ 与所有用户的相似度绝对值的和的倒数，即 $\frac{1}{\sum_{k=1} u_{ik}}$
• 计算过程
  1. 计算用户已评分商品的平均分 $v_i$
  2. 计算目标用户与其他用户的相似度 $u_ik = sim (u, v)$
     • 若没有相同的评分商品则 $sim(u,v) = NA$
  3. $v_{ij}^* = v_i + K \sum_{v_{kj \ne ?}} u_{ik}(v_{kj} - v_k)$

第四章 文本信息特征处理

特征提取

• 特征项
  • 特性
    • 能确实标识文本内容
    • 能将目标文本与其他进行区分
    • 个数不能太多
    • 特征项分离比较易实现
  • 特征抽取
    • 在不损伤文本核心内容的情况下，减少要处理的单词数，降低向量空间维度，简化计算，提升速度和效率
• 词级别的语义特征
  • 词频
    • 中频词更具代表性
    • 高频词区分较差
  • 词性
    • 动词和名词作为特征词
    • 虚词（感叹、介词等）要剔除
• 计算因素
  • 文档/词语长度
    • 长词汇含义更明确，更能反映主题
  • 词语直径
    • 首次出现与末次出现的距离（粗糙的度量特征）
  • 首次出现位置
    • 关键词一般较早出现
    • 越早出现，权重越大
    • 词语直径与首次出现位置选一个即可
  • 词语分布偏差
    • 词语在文章中的统计分布
    • 分布均匀的通常为重要词汇
• 汉语分词
  • 特点
    • 没有复数变化
    • 没有词边界
  • 方法
    • 正向/反向/双向最大匹配法
    • 问题
      • 歧义消除
      • 新词识别

特征子集选择

停用词过滤

• 去除对于分类没有贡献的特征项
• 手工/统计生成

文档频率阈值法 DF

• 齐夫定律
  • 单词按频率 $tf(t)$ 由高到低排列
  • 单词频率与序号近似反比 $rank(t) \cdot tf(t) \approx C$

TF-IDF

• 文档频率阈值法的补充改进
• $tfidf(t)=tf(t) \cdot idf(t)=tf(t) \cdot log \frac{n}{n(t)}$
  • $idf(t) = log \frac{n}{n(t)}$：包含特征项的样本在全部样本中的占比
  • $tf(t)$：特征项 $t$ 在所有训练样本中出现的次数 (出现频率)
  • $n(t)$：包含特征项 $t$ 至少一次的训练样本数
• 相比 DF，增加了包含特征项的样本在整体数据中的分布情况
  • 越多样本包含特征项，说明该特征项越重要，即 $log \frac{n}{n(t)}$ 越大

信噪比

• 信号强度与背景噪声的差值
• 信息熵 (整个系统的平均信息量) $Entropy (X) = -\sum_{i=1}^c p_i \ log \ p_i$
• 噪声 $Noise(t) = -\sum_{j=1}^n P(d_j,t) log P(d_j,t), \ 0 \leq Noise(t) \leq logn$
  • $P(d_j,t) = \frac{tf_{dj}(t)}{tf(t)}$：特征项 $t$ 出现在样本 $d_j$ 的可能
• 信噪比
  • $\displaylines{SNR(t) = log \ tf(t) - Noise(t) \\ = log \ tf(t) + \sum_{j=1}^n P(d_j,t)logP(d_j,t), \ 0 \leq SNR(t) \leq log \ tf(t)}$
    • 当且仅当特征项 $t$ 在全部样本中均出现 1 次时取得最小值， $SNR(t) = 0$
      • 说明全是噪声，没有贡献分类能力
    • 当特征项 $t$ 集中出现在 1 个样本中时取得最大值， $SNR(t) = log \ tf(t)$

信息增益

• C 的信息熵
  • $Entropy (C) = - \sum_{i=1}^k P(c_i) \ log P(c_i), \ P(c_i) = \frac{n_{ci}}{n}$
• C 关于 T 的条件信息熵
  • $\displaylines{Entropy (C|T) \\ =P(t)Entropy(C|t) + P(\overline t)Entropy(C|\overline t) \\ = - P(t) \sum_{i=1}^k P(c_i|t) \ log P(c_i|t) - P(\overline t) \sum_{i=1}^k P(c_i|\overline t) \ log P(c_i|\overline t), \ P(t) \\ = \frac{n(t)}{n}}$
• 信息增益
  • 信息熵与条件信息熵的差
  • $\displaylines{Gain(t) = Entropy(C) - Entropy(C|T) \\ = \sum_{i=1}^k P(c_i,t) \ log \frac{P(c_i,t)}{P(c_i)P(t)} + \sum_{i=1}^k P(c_i,\overline t) \ log \frac{P(c_i,\overline t)}{P(c_i)P(\overline t)}}$
    • $P(c_i,t) = \frac{n_{c_i}(t)}{n}$
      • 样本包含特征项 $t$ 且类别为 $c_i$
• 信息增益越小，说明对于分类的贡献越少，即去除

卡方统计($\chi^2$ 统计)

• 观察值与理论值间的偏离
• 特征对某类的 $\chi^2$ 统计值越高，与该类的相关性越大，携带类别信息越多
• $\chi^2 = \sum \frac{(O_i - E_i)^2}{E_i}$
  • 观测值 $O_i$
  • 理论值 $E_i = \frac{行总数 \times 列总数}{样本总数}$
• $\chi^2(t_i,C_j) = \frac{N \times (A \times D - C \times B)^2}{(A + C) \times (B + D) \times (A + B) \times (C + D)}$
  • $N = A + B + C + D$
  • 
  • $\chi^2 = \frac{[A - \frac{(A+C)(A+B)}{N}]^2}{\frac{(A+C)(A+B)}{N}} + \frac{[B - \frac{(B+D)(A+B)}{N}]^2}{\frac{(B+D)(A+B)}{N}} + \frac{[C - \frac{(A+C)(C+D)}{N}]^2}{\frac{(A+C)(C+D)}{N}} + \frac{[D - \frac{(B+D)(C+D)}{N}]^2}{\frac{(B+D)(C+D)}{N}}$

第五章 音频数据处理

• 响度级
  • 单位
    • 方
      • 1 方 = 1 kHz 的纯音 1 dB 的声压级
      • 人耳听阈对于 0 方
  • 人耳感知的声音响度是频率和声压级的函数
  • 主观等响度曲线
    • 
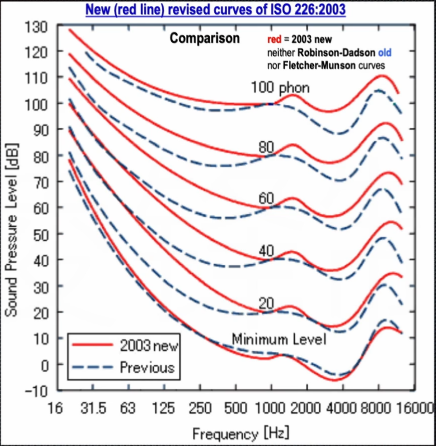
      • 每条红线上的点响度相同
• 掩蔽效应
  • 声音
    • 掩蔽音
      • 较强的声音
      • 纯音调
      • 宽带噪音
      • 窄带噪音
    • 被掩蔽音
      • 较弱的声音
  • 分类
    • 同时掩蔽/频域掩蔽
    • 异时掩蔽
      • 前掩蔽
      • 后掩蔽
• 采样率
  • 采样率越低，高频信息越少
  • 44.1 kHZ CD 最低标准
• 比特深度
  • 比特深度越大，动态范围越大，噪音越少
  • 16 bit 音乐发行格式
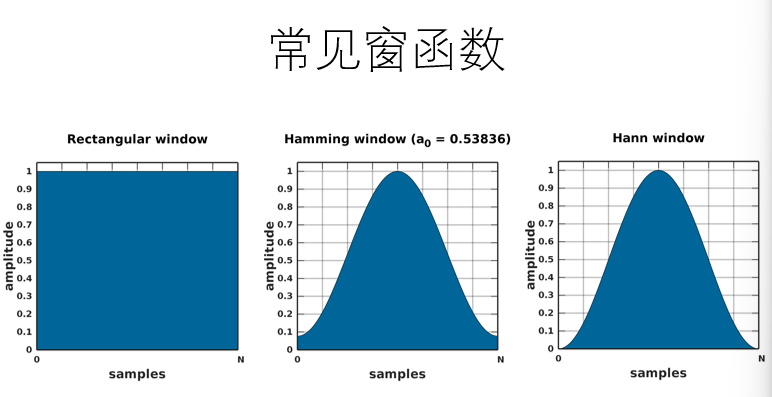
• 语音分帧
  • 
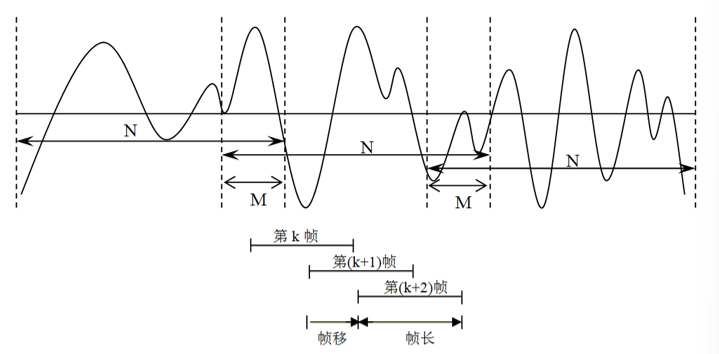
  • 使用一定长度的窗序列来截取
    • 
  • 每秒约取 33-100 帧
  • 为保证帧与帧之间平滑过渡，采用交叠分段
    • 帧移
      • 前后两帧交叠部分
    • 帧移与帧长比值取 0-0.5
• 短时过零率
  • 语音信号波形穿过横轴的次数
    • 连续信号，时域波形穿过时间轴
    • 离散信号，取样值改变符号
  • $Z_n = \frac{1}{2} \sum _{m=0}^{N-1} |sgn[x_n(m)] - sgn[x_n(m-1)]|$

第六章 图像信息特征抽取

图像表示

• 矩阵表示
  • 灰度图像
    • $M \times N$ 的矩阵存灰度值
    • 0（全黑）
    • 255（全白）
  • 彩色图像
    • RGB 通道分为三个矩阵
    • 矩阵叠加生成图像

颜色直方图特征

• 反映特定图像中的颜色级与出现该种颜色的概率之间关系的图形
• 灰度直方图函数 $Hist(I_k) = \frac{n_k}{M \times N} \ 1 \leq k \leq K$
  • $I_k$：第 $k$ 个灰度级
    • $K$ 值越高灰度过渡越多，细节更细致
    • $K$ 值越低灰度过渡越少，细节更模糊，难以分辨
  • $n_k$：图像中 $I_k$ 灰度级的像素点总数
  • 分母用来进行归一化处理
• 颜色直方图函数 $Hist(C_{r,g,b}) = \frac{n_{r,g,b}}{M \times N} \ 1 \leq r \leq R,\ 1 \leq g \leq G,\ 1 \leq b \leq B$
  • $C_{r, g, b}$ ：第（r, g, b）个颜色柄
  • $n_{r,g,b}$ ：$C_{r, g, b}$ 的像素点总数
  • 分母用来进行归一化处理
• 计算流程
  1. 颜色量化
     • 将颜色空间划分成若干个颜色区间，每个区间代表一个颜色柄
     • 均匀量化
       • 对每个颜色分量的划分是均匀的
  2. 统计颜色柄中像素点总数
  3. 计算颜色直方图 $Hist(C_{r,g,b}) = \frac{n_{r,g,b}}{M \times N} \ 1 \leq r \leq R,\ 1 \leq g \leq G,\ 1 \leq b \leq B$
• 特征特点
  • 优点
    • 提取方法简单，计算复杂度小
    • 图像操作（位移、旋转、镜像等）不会影响该特征
  • 局限
    • 颜色空间的选取
      • 颜色空间
        • RGB？
        • HSV？
        • CIE-Lab？
      • RGB 不符合人类对颜色相似的主观判断
    • 量化方法制定
      • 如何去点个量化的阶数 $K$

颜色聚合矢量特征

• 引入一定空间信息进一步区分颜色分布类似而空间分布不同的图像
• 计算流程
  1. 将颜色空间划分成若干个柄
  2. 颜色柄
     • 连贯点 $con_i$
       • 颜色相同
       • 空间连续
     • 离散点 $dis_i$
     • 第 $i$ 个颜色柄的颜色聚合对 $(\alpha_i,\beta_i)$
       • $\alpha_i = \frac{con_i}{M \times N}$
       • $\beta_i = \frac{dis_i}{M \times N}$
  3. 图像的颜色聚合矢量特征 $\langle (\alpha_1,\beta_1),(\alpha_2,\beta_2),\dots,(\alpha_K,\beta_K) \rangle$
     • $K$：颜色柄总数
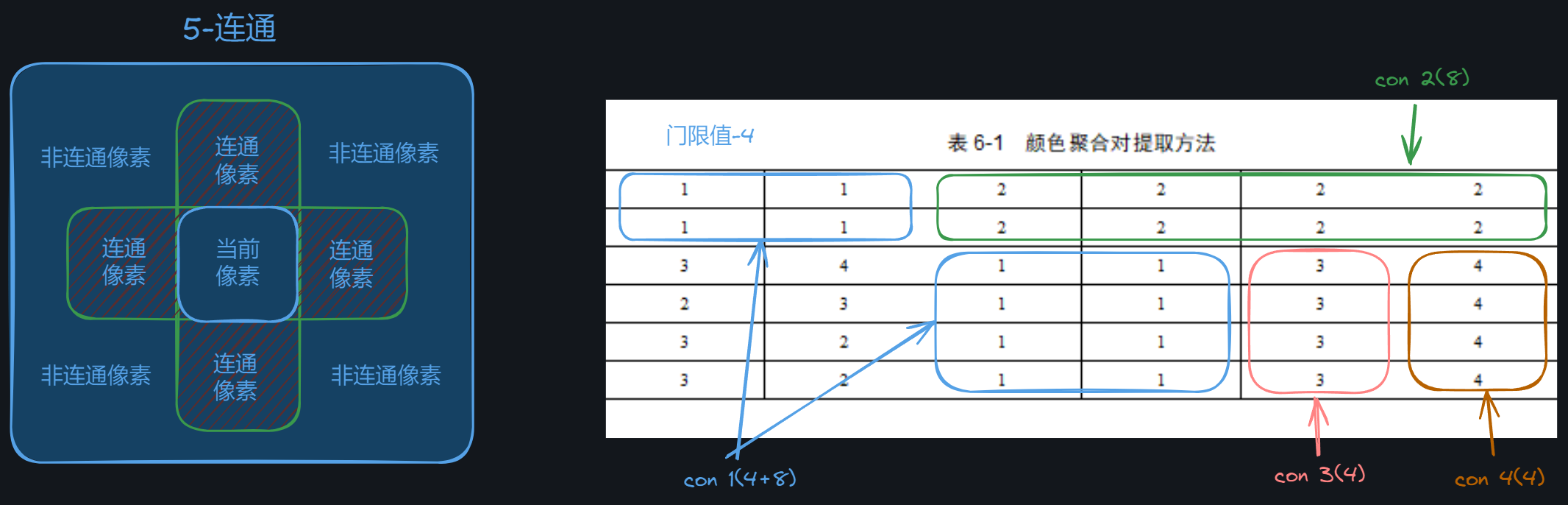
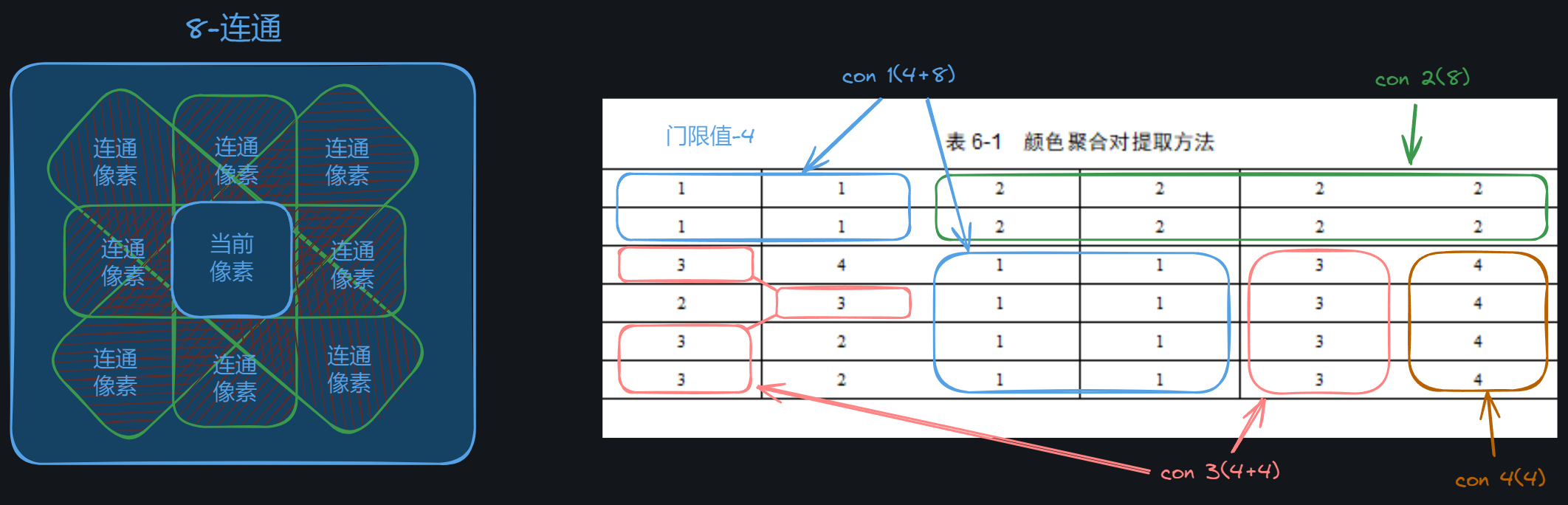
  • 连贯点与离散点的计算
    • 门限 threshold
      • 区分是否连续
    • 5-连通
      • 
        • $\displaylines{con_1 = 12, \ dis_1 = 0 \Rightarrow \alpha_1 = \frac{12}{36},\beta_1 = 0 \\ con_2 = 8, \ dis_2 = 3 \Rightarrow \alpha_2 = \frac{8}{36},\beta_2 = \frac{3}{36} \\ con_3 = 4, \ dis_3 = 4 \Rightarrow \alpha_3 = \frac{4}{36},\beta_3 = \frac{4}{36} \\con_4 = 4, \ dis_4 = 1 \Rightarrow \alpha_4 = \frac{4}{36},\beta_4 = \frac{1}{36}}$
    • 8-连通
      • 
        • $\displaylines{con_1 = 12, \ dis_1 = 0 \Rightarrow \alpha_1 = \frac{12}{36},\beta_1 = 0 \\ con_2 = 8, \ dis_2 = 3 \Rightarrow \alpha_2 = \frac{8}{36},\beta_2 = \frac{3}{36} \\ con_3 = 8, \ dis_3 = 0 \Rightarrow \alpha_3 = \frac{8}{36},\beta_3 = 0 \\ con_4 = 4, \ dis_4 = 1 \Rightarrow \alpha_4 = \frac{4}{36},\beta_4 = \frac{1}{36}}$
• 局限性
  • 颜色空间选取和空间量化方法的制定
  • 离散/连贯的门限值设定
  • 连续性判断导致计算复杂度变高

颜色矩

• 引入低阶矩描述整个图像的颜色变化
• 常用颜色矩
  • 一阶矩-颜色均值
    • $\mu_i=\frac{1}{N \times M} \sum_{j=1}^{N \times M}c_{ij}$
      • $c_{ij}$：像素点 $j$ 的第 $i$ 个颜色通道的颜色值
        • $i$ 一般取 $1 \sim 3$，代表 RGB 三个通道
  • 二阶矩-颜色标准差
    • $\sigma_i=(\frac{1}{N \times M} \sum_{j=1}^{N \times M}(c_{ij}-\mu_i)^2)^{\frac{1}{2}}$
  • 三阶矩-颜色偏度
    • $s_i=(\frac{1}{N \times M} \sum_{j=1}^{N \times M}(c_{ij}-\mu_i)^3)^{\frac{1}{3}}$
• 特点
  • 常规 RGB 图像仅需 $3 \times 3 = 9$ 维，相比其他颜色特征，维数最低
  • 仅包含颜色信息，缺乏对细节的描述

第七章 信息处理模型和算法

文本匹配

单模式匹配

• 过程
  • 匹配
  • 后移
• 算法
  • Brute-Force 算法（暴力）
    • 最坏时间复杂度 $O(m * n)$
    • 将正文分为 $n-m+1$ 个长度为 $m$ 的子串
      • 相当于每次后移一位进行匹配
    • 检查每个子串是否与模式串 P 匹配
    • 对模式串扫描常常需要回溯，存在许多重复操作，影响效率
  • KMP 算法
    • 三个人的名字
      • Knuth
      • Morris
      • Pratt
    • 通过已匹配的部分来决定后移的位数
      • 匹配表
        • 模式串对自己进行处理生成的匹配表
          • “部分匹配值”就是”前缀”和”后缀”的最长的共有元素的长度
          • 
      • 移动位数 = 已匹配的字符数 - 对应的部分匹配值
    • 时间复杂度
      • 预处理阶段 $O(m)$
      • 平均查找复杂度 $O(m + n)$
      • 最坏情况下 $O(2n)$
      • $m$：匹配字符串长度
      • $n$：完整字符串长度，$n \geq m$
  • QS 算法

多模式匹配 DFSA 算法

机器学习分类

线性分类器

• 通过一个线性判别函数的输出来确定数据类别
  • 
  • $D=\sum_{i=1}^n w_ix_i + w_0$
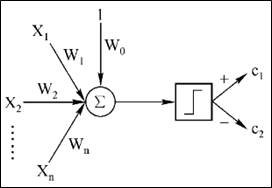
    • 输出为正，判别为一类
    • 输出为负，判别为另一类
    • 输出 0，不能做出判断
• 特点
  • 线性分类器结构相对简单，学习优化过程计算复杂度低
  • 泛化能力较强
  • 存在分布不可线性分割的情况

最临近分类法 KNN

• 通过测试样本和训练样本间的距离来进行分类
  • $dist(X,S_{ij}) = ||X-S_{ij}|| \ i = 1,2,\dots,C,\ j = 1,2,\dots,n_i$
    • $C$：类别总数
    • $S_i$：第 $i$ 类训练样本集
    • $X$：测试样本
  • 计算与测试样本的距离，选择最接近的 $k$ 个样本点组成 $N$
    • 测试样本即分类为 $N$ 中个数最多的类别
• 特点
  • 不需要复杂学习优化过程，但需要计算距离，存在一定计算量
  • 在一定程度上，可以处理分布较为复杂多样的问题
    • 与线性分类器相比，分界面并不是一个超平面，可以是更为复杂的曲线

线性可分支持向量机

• 通过间隔最大化学习得到分离超平面
  • 分离超平面 $\omega^* \cdot x + b^* = 0$
  • 分类决策函数 $f(x) = sign(\omega^* \cdot x + b^*)$
    • $sign()$：用来判断正负
• 点到分离超平面的远近可以表示分类预测的确信程度
  • 函数间隔 $\hat \gamma_i = y_i(\omega \cdot x_i + b)$
    • 超平面定义
      • 所有样本点的函数间隔最小值 $\hat \gamma = \underset{i = 1,\dots ,N}{min} \hat \gamma_i$
  • 几何间隔 $\gamma_i = y_i(\frac{\omega}{||\omega||} \cdot x_i + \frac{b}{||\omega||})$
    • $||\omega||$ 表示 $\omega$ 向量模长
    • 超平面定义
      • 所有样本点的几何间隔最小值 $\gamma = \underset{i = 1,\dots ,N}{min} \gamma_i$
  • 函数间隔与几何间隔 $\gamma_i = \frac{\hat \gamma_i}{||\omega||}$ $\gamma = \frac{\hat \gamma}{||\omega||}$
  • 间隔最大化
    • 间隔越大，分类确信度越高
    • 计算转化
      • 计算最大几何间隔
        • $\displaylines{\underset{\omega,b}{max} \ \gamma \\ s.t. \ y_i(\frac{\omega}{||\omega||} \cdot x_i + \frac{b}{||\omega||}) \geq \gamma, i = 1,2,\dots,N}$
      • 几何间隔转为函数间隔
        • $\displaylines{\underset{\omega,b}{max} \ \frac{\hat \gamma}{||\omega||} \\ s.t. \ y_i(\omega \cdot x_i + b) \geq \hat \gamma, i = 1,2,\dots,N}$
      • 转化为最小值问题（最优化问题）, 方便计算
        • $\displaylines{\underset{\omega,b}{min} \ \frac{1}{2}||\omega||^2 \\ s.t. \ y_i(\omega \cdot x_i + b)-1 \geq 0, i = 1,2,\dots,N}$
• 求解分离超平面
  • 求最优化问题的最优解 $\omega^*$ 和 $b^*$
  • 得到分离超平面 $\omega^* \cdot x + b^* = 0$ 和分类决策函数 $f(x) = sign(\omega^* \cdot x + b^*)$
• 支持向量
  • 
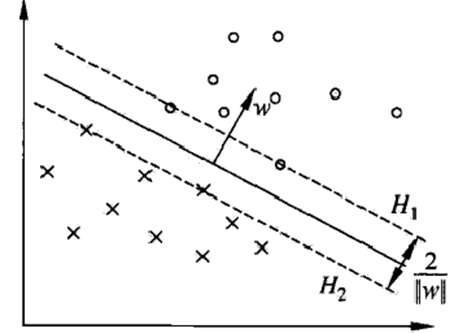
  • 分布在间隔边界处的样本点，使约束条件等号成立的点
  • 正例的支持向量在 $H_1 = \omega \cdot x + b = 1$
  • 负例的支持向量在 $H_2 = \omega \cdot x + b = -1$
  • $H_1$ 和 $H_2$ 为间隔边界
• 对偶算法
  • 用于求解最优化算法
  • 引入核函数，推广到非线性分类问题
  • 拉格朗日函数
    • $L(\omega,b,\alpha)=\frac{1}{2}||\omega||^2-\sum_{i=1}^N \alpha_i y_i(\omega \cdot x_i + b) + \sum_{i=1}^N \alpha_i$
      • $\alpha = (\alpha_1,\alpha_2,\dots,\alpha_N)^T$
    • 根据拉格朗日对偶性，求解 $\underset{\alpha}{max} \ \underset{\omega,b}{min} \ L(\omega,b,\alpha)$
      • 先求 $\underset{\omega,b}{min} L(\omega,b,\alpha)$
        • 分别对 $\omega$ 和 $b$ 求偏导并令其等于 0
        • 得到 $\underset{\omega,b}{min} \ L(\omega,b,\alpha) = -\frac{1}{2}\sum_{i=1}^N \sum_{j=1}^N \alpha_i\alpha_j y_i y_j(x_i \cdot x_j) + \sum_{i=1}^N \alpha_i$
      • 再算 $\underset{\omega,b}{min} L(\omega,b,\alpha)$ 的对 $\alpha$ 极大值问题 (对偶问题)
        • $\displaylines{\underset{\alpha}{max} \ -\frac{1}{2}\sum_{i=1}^N \sum_{j=1}^N \alpha_i\alpha_j y_i y_j(x_i \cdot x_j) + \sum_{i=1}^N \alpha_i \\ s.t. \sum_{i=1}^N \alpha_i y_i = 0 \\ \alpha_i \geq 0,i=1,2,\dots,N}$
        • 等价对偶最优化问题 $\displaylines{\underset{\alpha}{min} \ \frac{1}{2}\sum_{i=1}^N \sum_{j=1}^N \alpha_i\alpha_j y_i y_j(x_i \cdot x_j) - \sum_{i=1}^N \alpha_i \\ s.t. \sum_{i=1}^N \alpha_i y_i = 0 \\ \alpha_i \geq 0,i=1,2,\dots,N}$
          • 注意限制条件，计算时用于消元
      • 计算解得 $\alpha$
• 计算分离超平面和分类决策函数
  • $\omega^* = \sum_{i=1}^N \alpha_i^* y_i x_i$
  • $b^* = y_j - \sum_{i=1}^N \alpha_i^* y_i (x_i \cdot x_j)$
    • 代入计算时，$j$ 可任取一个训练数据
  • 分离超平面 $\sum_{i=1}^N \alpha_i^* y_i (x \cdot x_i) + b^* = 0$
  • 分类决策函数 $f(x) = sign(\sum_{i=1}^N \alpha_i^* y_i (x \cdot x_i) + b^* = 0)$
  • 计算流程
    • 求解最优化问题 $\displaylines{\underset{\alpha}{min} \ \frac{1}{2}\sum_{i=1}^N \sum_{j=1}^N \alpha_i\alpha_j y_i y_j(x_i \cdot x_j) - \sum_{i=1}^N \alpha_i \\ s.t. \sum_{i=1}^N \alpha_i y_i = 0 \\ \alpha_i \geq 0,i=1,2,\dots,N}$，得到 $\alpha$
    • 代入计算 $\omega$ 和 $b$
    • 得到分离超平面和分类决策函数

朴素贝叶斯 SVM

• 计算训练集中的各特征分类的概率，再通过比较条件概率来确定
• 计算过程
  • 极大似然估计
    • 先计算各特征分类的概率
      • $P(Y=c_k)$ 通过统计数据集得到
        • 数据集中共 15 条数据，Y=1 有 7 条，Y=-1 有 8 条
        • $P(Y=1)=\frac{7}{15},P(Y=-1)=\frac{8}{15}$
      • $P(X^{(j)} = x^{(j)}|Y = c_k) = \frac{N_{x_j,c_k}}{N}$
        • $N_{x_j,c_k}$：数据集中特征为 $x_i$ 且为 $c_k$ 类的数据数
    • 计算条件概率
      • $P(Y = c_k|X=(x^{(1)}，x^{(2)}，\dots,x^{(n)})) = P(Y = c_k) \prod_{j=1}^n P(X^{(j)} = x^{(j)}|Y = c_k)$
        • 假设独立性
          • 假设各特征之间相互独立，得到 $P(X^{(1)} = x^{(1)},X^{(2)} = x^{(2)},\dots,X^{(n)} = x^{(n)})|Y = c_k) = \prod_{j=1}^n P(X^{(j)} = x^{(j)}|Y = c_k)$
    • 算出所有分类的条件概率后，概率最大的分类即为分类结果
  • 贝叶斯估计
    • 极大似然估计可能会因为数据集中缺失，导致概率为 0
    • $P(Y=c_k)$ 相比极大似然估计，在分子和分母上增加一项避免概率为 0
      • $P(Y=c_k) = \frac{N_{c_k} + \lambda}{N+K\lambda}$
        • $N_{c_k}$：数据集中的统计量
        • $K$：类别个数
      • $P(X^{(j)} = x^{(j)}|Y=c_k) = \frac{N_{x_j} + \lambda}{N+S_j \lambda}$
        • $S_j$：特征可取值
      • $\lambda$：默认取 1
    • 算出所有分类的条件概率后，概率最大的分类即为分类结果

决策树

• 树形结构
  • 结点
    • 内部结点
      • 特征/属性
    • 叶结点
      • 类
  • 有向边
• 从根结点开始，递归选择最优的特征，直至实例分到叶结点的类中
• 常用算法
  • ID3
  • C4.5
  • CART
• ID3 算法
  • 结合信息增益，选择信息增益最大的作为结点，并建立子结点
  • 经验熵 $H(D)$
    • $H(D) = -\sum_{k=1}^K \frac{|C_k|}{|D|}log_2 \frac{|C_k|}{|D|}$
  • 经验条件熵 $H(D|A)$
    • $H(D|A) = \sum_{i=1}^n \frac{|D_i|}{|D|}H(D_i) = -\sum_{i=1}^n \frac{|D_i|}{|D|} \sum_{k=1}^K \frac{|C_k|}{|D|}log_2 \frac{|C_k|}{|D|}$
  • 信息增益
    • $g(D,A) = H(D) - H(D|A)$
  • 计算下个结点的信息增益时，要去掉父结点其他子结点的数据
    • 若当前为 no，则要去掉 yes 分支的数据

第十章 社交网络

• 在线社交网络的核心要素
  • 网络群体
  • 关系结构
    • 信息内容
• 信息内容特点
  • 多样性
    • 信息内容的话题不受限制
    • 用户可以讨论任何话题
    • 时时刻刻也会产生新的话题
  • 平等性
    • 用户可以平等的发布和传播信息内容
  • 迅捷性
    • 信息的发布和接受都非常方便
    • 信息传播的距离极大缩短
  • 蔓延性
    • 信息内容的传播呈核裂变式，几何级数的增长

个体影响力计算

度中心性

• 网络内节点与邻居节点连边的数量
• 节点的邻居节点越多，该节点的影响力越大
• 

介数中心性

• 一个节点成为其他任意两个节点最短路径上的必经之路的次数越多，重要性越大
• $b(i)=\sum_{p \ne i \ne q}^n \frac{g_{pg}(i)}{g_{pq}}$
  • $g_{pg}$：节点 p 到节点 q 最短路径的数目
  • $g_{pg}(i)$：节点 p 到节点 q 最短路径中经过节点 i 的路径的数目
• 计算复杂度过高，无法快速计算

接近中心性

• 考察节点到任意节点最短路径的平均长度
• $c(i) = \frac{n-1}{\sum_{j \ne i} st_{ij}}$
  • $st_{ij}$：节点 i 和节点 j 之间的最短距离
• 需要计算所有节点之间的最短路径长度，计算复杂度高

LH-index 算法

• 邻居节点的影响水平越高，该节点的影响力越高
• h 指数
  • 衡量学者学术影响力
  • h 篇被引用的论文，每篇都被引用至少 h 次
• $LH(i) = w_i h(i) + w_2 \sum_{v \in N(i)} h(v)$
  • $N(i)$：邻居节点的集合
  • $w_1$ 和 $w_2$：节点的比重，按需进行调整

PageRank 算法

• 与 [[0x03_Note/0x00_Content Security/信息内容安全#|信息检索部分的PageRank]] 是相同的
• TwitterRank 算法
  • 矩阵 DT
    • $\begin{bmatrix} DT_{11} & \cdots & DT_{1m} \\ \vdots & \ddots & \vdots \\ DT_{n1} & \cdots & DT_{nm} \end{bmatrix}$
      • $DT_{ij}$：第 i 个用户在第 j 个话题中的发帖数量
    • 归一化处理
      • 行归一化
        • $\sum_{j=1}^m DT_{ij} = 1$
        • 记为 $DT_{ij}'$，i 用户参与话题的概率
        • eg
          • $DT_{21} = 2,DT_{22} = 3,DT_{23} = 5$
          • $DT_{21}+DT_{22}+DT_{23}=1$
          • $DT_{21}' = \frac{2}{10},DT_{22}' = \frac{3}{10},DT_{23}' = \frac{5}{10}$
      • 列归一化
        • $\sum_{i=1}^n DT_{ij} = 1$
        • 记为 $DT_{ij}''$，j 话题中用户参与的概率
        • eg
          • $DT_{12} = 2,DT_{22} = 3,DT_{32} = 4$
          • $DT_{12}+DT_{22}+DT_{32}=1$
          • $DT_{12}'' = \frac{2}{9},DT_{22}'' = \frac{3}{9},DT_{32}'' = \frac{4}{9}$
  • 相似度 $sim_t(i,j)$
    • $sim_t(i,j) = 1 - |DT_{it}' - DT_{jt}'|$
      • 如果用户 i 关注用户 j，两者在 t 话题下的相似度
  • 转移概率 $p_t (i, j)$
    • $p_t(i,j) = \frac{|T_j|}{\sum_{s_a} |T_a|} \cdot sim_t(i,j)$
      • $|T_j|$：用户 j 在话题 t 下发布的所有博文数量
      • $\sum_{s_a} |T_a|$：用户 i 在所有好友的话题 t 下发布的所有博文数量
    • 转移矩阵
      • $\begin{bmatrix} P_t(1,1) & P_t(1,2) & \cdots & P_t(1,n) \\ \vdots & \vdots & \vdots & \vdots \\ P_t(n,1) & P_t(n,2) & \cdots & P_t(n,n) \end{bmatrix}$
  • 用户 i 不一定关注用户 j 的情况
    • 用户 i 的影响力矩阵
      • $E_t = DT_t''$
        • $DT_t''$：$DT''$ 的第 t 列
    • 影响力 $\pi = qp_t \pi + (1-q)E_t$
      • $qp_t \pi$：关注情况
      • $(1-q)E_t$：未关注情况

信息传播模型

独立级联模型 ICM

• ICM 计算出的是概率值
• 有向图 $G(V,E)$
  • $V$：用户
    • 激活状态
    • 未激活状态
  • $e=(u,v) \in E$
    • e ：u-v 之间的边
• 激活概率 $P(u,v)$
  • u 激活 v
    • $P(u,v)$
  • u 未激活 v
    • $1 - P(u,v)$
  • 激活概率 $P(u,v)$
    • 随机取值
      • $P(u,v) \in [0,1]$
    • 较小的固定取值
      • 0.1
      • 0.01
      • 0.001
      • …
    • 入户线数倒数取值
      • $P(u,v) = \frac{1}{|N_{in}(v)|}$
        • $|N_{in}(v)|$：（有向边）入户线数目
    • 固定随机取值
      • $P(u,v) \in \{0.1,0.01,0.001\}$
• 激活过程
  • t=0 时刻，仅有种子集合 $S$
    • 种子集合 S：初始激活的用户
  • 当用户 u 在 t 时刻被激活，用户 u 仅可在 t+1 时刻激活其他用户
    • 通俗解释
      • 用户获得信息后，会在第一时间进行转发，而不是等一段时间后再转发
      • 所以在模型中仅能在 t+1 时刻激活其他用户是符合传播过程的
  • 激活状态 $S_u(t)$
    • $S_u(t) = 1$
      • 在 t 时刻被首次激活
    • $S_u(t) = 0$
      • 未被激活
      • 在 t 时刻前已被激活
    • 激活应该是不可逆的
      • 接收到信息后，就会被激活
  • 激活概率 $P_r$
    • $P_r(S_v(t) = 1) = 1 - \prod_{u \in N_{in}(v)}[1 - S_u(t-1) \cdot P(u,v)]$
      • t 时刻，v 被激活，需要 u 在 t-1 时刻被激活
      • u 属于 v 的父结点集合

线性阈值模型 LTM

• LTM 计算出的是确定值
• 父节点 u 对子节点 v 的影响力权重，且和小于等于 1
• 激活条件
  • $\sum_{u \in N_{in}(v),u is active} b_{u,v} \geq \theta_v$
  • v 的所有父节点的影响力权重累积超过阈值 $\theta_v$，$\theta_v \in [0,1]$
  • $\theta_v$ 越大，节点 v 越难被影响，即越难被激活
• 激活过程
  • t=0 时刻，仅有种子集合 $S$
  • 逐时刻进行判断是否满足上激活条件
  • 若没有新的被激活节点出现，则传播过程结束
• 当网络结构、$b_{u,v}$、$\theta_v$ 和 $S$ 不变，那么整个传播过程都将是确定、不会改变的

传染病模型

• 模拟节点感染和恢复
• 常见模型
  • SI
  • SIR
  • SIRS
    • SEIR
• 节点分类
  • S 类 - 易感者
    • 未被激活，易被激活
  • E 类 - 暴露者
    • 被激活，但无法激活其他节点
  • I 类 - 感染者
    • 被激活，可以激活其他 S 类节点为 E 类或 I 类节点
  • R 类 - 康复者
    • 重新变为 S 类节点