Ch9.差分隐私变体

提出差分隐私变体的目的是为了更加紧致隐私消耗量.

之前所提到的隐私消耗量的计算方法, 得到的都是较为宽松的上界, 而实际的消耗远低于计算出的上界.

9.1 最大散度和瑞丽散度

1. 最大散度 Max Divergence

   在统计学中, 散度是用来度量两种概率分布差异的方法.
   最大散度是 KL 散度(Kullback-Leibler Divergence)的最坏情况.
   两个概率分布 $Y$ 和 $Z$ 的最大散度定义为:

   $$D_{\infty}(Y \parallel Z) = \underset{S \subseteq Supp(Y)}{max} \Biggl[ log \frac{Pr[Y \in S]}{Pr[Z \in S]} \Biggr]$$

   若证明:

   $$D_{\infty}(F(x) \parallel F(x')) \leq \epsilon$$

   则 $F$ 满足 $\epsilon$-差分隐私.

2. 瑞丽散度 Rényi Divergence
   概率分布 $P$ 和 $Q$ 的 $\alpha$ 阶瑞丽散度定义为:

   $$D_{\alpha}(P \parallel Q) = \frac{1}{\alpha - 1} log E_{x \sim Q} \Bigl( \frac{P(x)}{Q(x)} \Bigr)^{\alpha}$$

   $P(x)$ 和 $Q(x)$ 分别为 $P$ 和 $Q$ 在 $x$ 处的概率密度.

9.2 瑞丽差分隐私

瑞丽差分隐私 Rényi Differential Privacy RDP
如果对与所有的临近数据集 $x$ 和 $x'$, 随机机制 $F$ 满足:

则机制 $F$ 满足 ($\alpha$, $\bar \epsilon$)-RDP.

$\bar \epsilon$ 用于区别 $\epsilon$-差分隐私 和 ($\epsilon$,$\delta$)-差分隐私的 $\epsilon$.

如果机制 $F$ 满足 ($\alpha$, $\bar \epsilon$)-RDP, 那对于任意给定的 $\delta > 0$, $F$ 满足 ($\epsilon$,$\delta$)-差分隐私.
其中 $\epsilon = \bar \epsilon + \frac{log(\frac{1}{\delta})}{\alpha - 1}$, $\delta$ 应选择一个有意义的值, 如 $\delta \leq \frac{1}{n^2}$.

实现瑞丽差分隐私的基本机制是高斯机制.
对于一个 $L2$ 敏感度为 $\Delta f$ 的函数 $f$: $\mathcal{D} \rightarrow \mathbb{R}^k$. 构造 ($\alpha$, $\bar \epsilon$)-瑞丽差分隐私机制:

满足瑞丽差分隐私的高斯机制:

def gaussian_mech_RDP_vec(vec, sensitivity, alpha, epsilon_bar): 
    sigma = np.sqrt((sensitivity**2 * alpha) / (2 * epsilon_bar)) 
    return [v + np.random.normal(loc=0, scale=sigma) for v in vec]

RDP 的主要优势
用高斯机制实现的瑞丽差分隐私满足紧致组合性, 组合使用机制时不需要引入特殊的高级组合定理.

RDP 的串行组合性

$F_1$ 满足 ($\alpha$, $\bar \epsilon_1$)-RDP.
$F_2$ 满足 ($\alpha$, $\bar \epsilon_2$)-RDP.
$F_1$ 和 $F_2$的组合机制满足 ($\alpha$, $\bar \epsilon_1 + \bar \epsilon_2$)-RDP.

给定噪声级别(即给定 $\sigma^2$)时, 先使用这个串行组合性, 限制重复应用高斯机制的隐私消耗, 再将隐私定义转换为 ($\epsilon$, $\delta$)-差分隐私.

这个方法比直接在 ($\epsilon$, $\delta$) 中应用串行组合(甚至高级组合)的总消耗量要低很多.

9.3 零集中差分隐私

零集中差分隐私 Zero-concentrated Differential Privacy zCDP

零集中差分隐私也是基于瑞丽散度定义的差分隐私变体, 但仅包含一个隐私参数 $\rho$.
对于所有的临近数据集 $x$ 和 $x'$, 以及所有的 $\alpha \in (1,\infty)$, 如果一个随机机制 $F$ 满足:

则 $F$ 满足 $\rho$-零集中差分隐私.

零集中差分隐私的定义比瑞丽差分隐私更强, 零集中差分隐私对瑞丽散度的阶有更严格的限制. 随着 $\alpha$ 的增大, 限制会变宽松.
零集中差分隐私和瑞丽差分隐私相同, 也可以转换为 ($\epsilon$, $\delta$)-差分隐私. $\delta > 0, \epsilon = \rho + 2 \sqrt{\rho \ log (\frac{1}{\delta})}$.

零集中差分隐私也可以使用高斯机制实现, 对于一个 $L2$ 敏感度为 $\Delta f$ 的函数 $f$: $\mathcal{D} \rightarrow \mathbb{R}^k$.

def gaussian_mech_zCDP_vec(vec, sensitivity, rho): 
    sigma = np.sqrt((sensitivity**2) / (2 * rho)) 
    return [v + np.random.normal(loc=0, scale=sigma) for v in vec]

zCDP 的串行组合性

$F_1$ 满足 $\rho_1$-zCDP.
$F_2$ 满足 $\rho_2$-zCDP.
$F_1$ 和 $F_2$的组合机制满足 $\rho_1 + \rho_2$-zCDP.

9.4 不同差分隐私变体的组合性

当遇到以下情况时, 使用差分隐私变体:

使用高斯机制实现差分隐私(特别是高维向量)
问询算法多次(成百上千次)使用差分隐私机制

不同差分隐私的总隐私消耗量比较
示例算法: 一个应用 $k$ 次高斯机制的问询算法.
固定 $\sigma$ (固定每轮迭代中高斯机制引入的噪声量)的取值.
固定 $\delta$ 的取值.

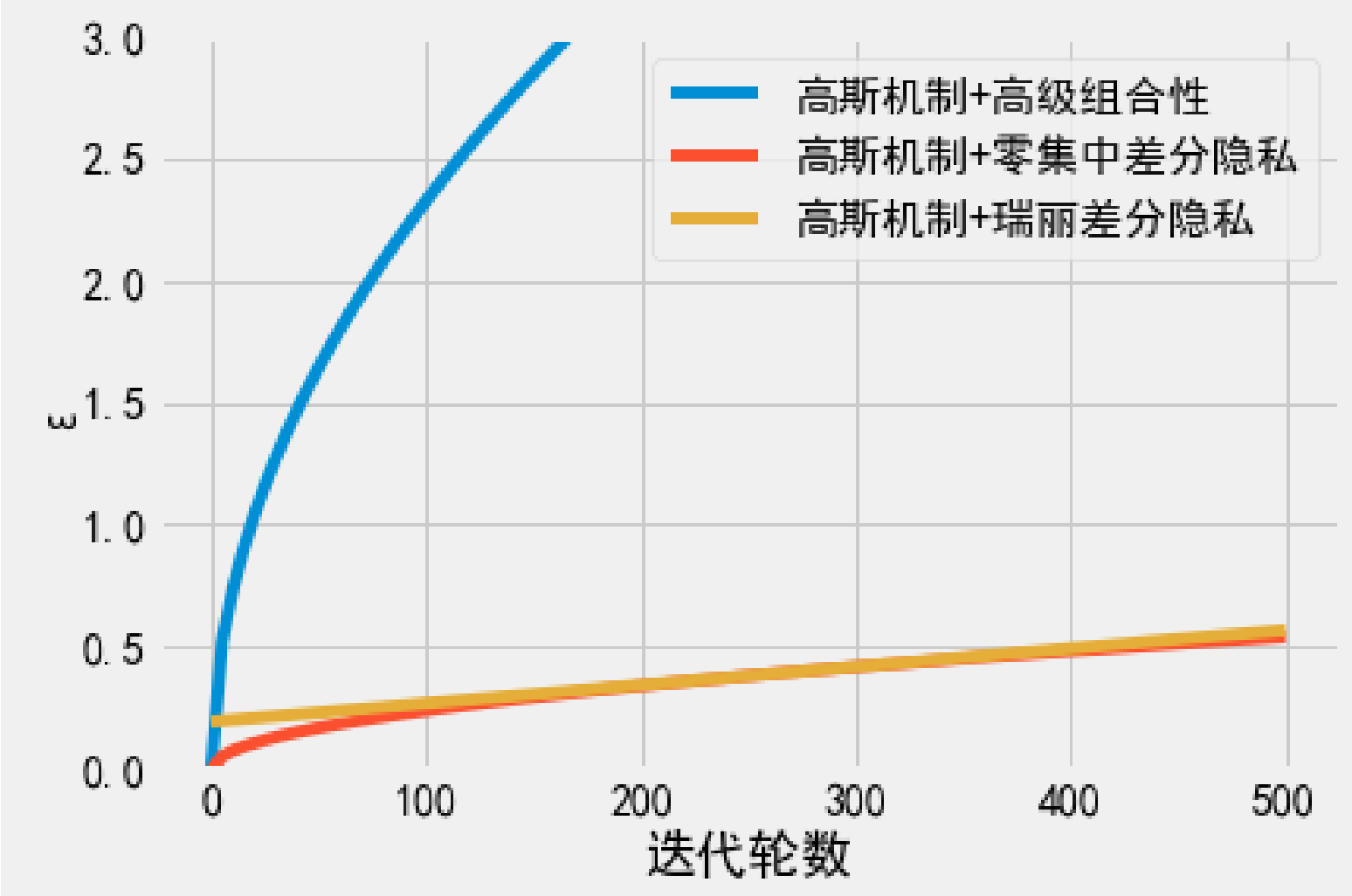
• 首先可以明显的发现, zCDP 和 RDP 的串行组合性都比应用高级组合性的 ($\epsilon$, $\delta$)-差分隐私的总消耗量好得多.
• RDP 固定了 $\alpha$, RDP 的 $\epsilon$ 值会随着 $k$ 的增加而线性增加; zCDP 会同时考虑多个 $\alpha$, zCDP 的 $\epsilon$ 值会随着 $k$ 的增加而次线性增加.

  次线性增加: 函数增长速度比线性函数更慢.

• 两条曲线会相交, 相交点由 RDP 的 $\alpha$ 值决定.
  (图中 $\alpha$ 为 20, 两条曲线大概在 $k = 300$ 时相交)

RDP 要谨慎的选择 $\alpha$ 值, 进而得到更紧致的消耗量. 通过测试多个 $\alpha$ 值, 观察哪个 $\alpha$ 值的消耗量最小. 该测试仅与选择的隐私参数和迭代次数有关, 与数据本身无关. 可根据需要测试任意数量的 $\alpha$, 不会增加额外的隐私消耗. 一般测试少量 $\alpha$ 值即可找到 $\epsilon$ 的最小值 ($\alpha \in [2 , 100]$).