近似差分隐私 Approximate Differential Privacy / ()-差分隐私:
是输出不满足近似差分隐私的失败概率. 即能够满足差分隐私的概率为 1-.
因为是不满足差分隐私的情况, 所以 的取值要很小, 一般要求 (n 为数据集总大小).
失败不会产生类似泄露整个数据集的严重后果.
7.1 近似差分隐私的性质
近似差分隐私也具有串行组合性, 和 要分别相加.
满足 (, )-差分隐私.
满足 (, )-差分隐私.
满足 (, )-差分隐私.
7.2 高斯机制
高斯机制可以替代拉普拉斯机制. 使用高斯噪声替代拉普拉斯噪声.
高斯机制无法满足 -差分隐私, 但可以满足 ()-差分隐私.
使用高斯机制得到的满足 ()-差分隐私
为 的敏感度.
表示均值为 0, 方差为 的高斯(正态)分布的采样结果.
高斯机制与拉普拉斯机制的对比
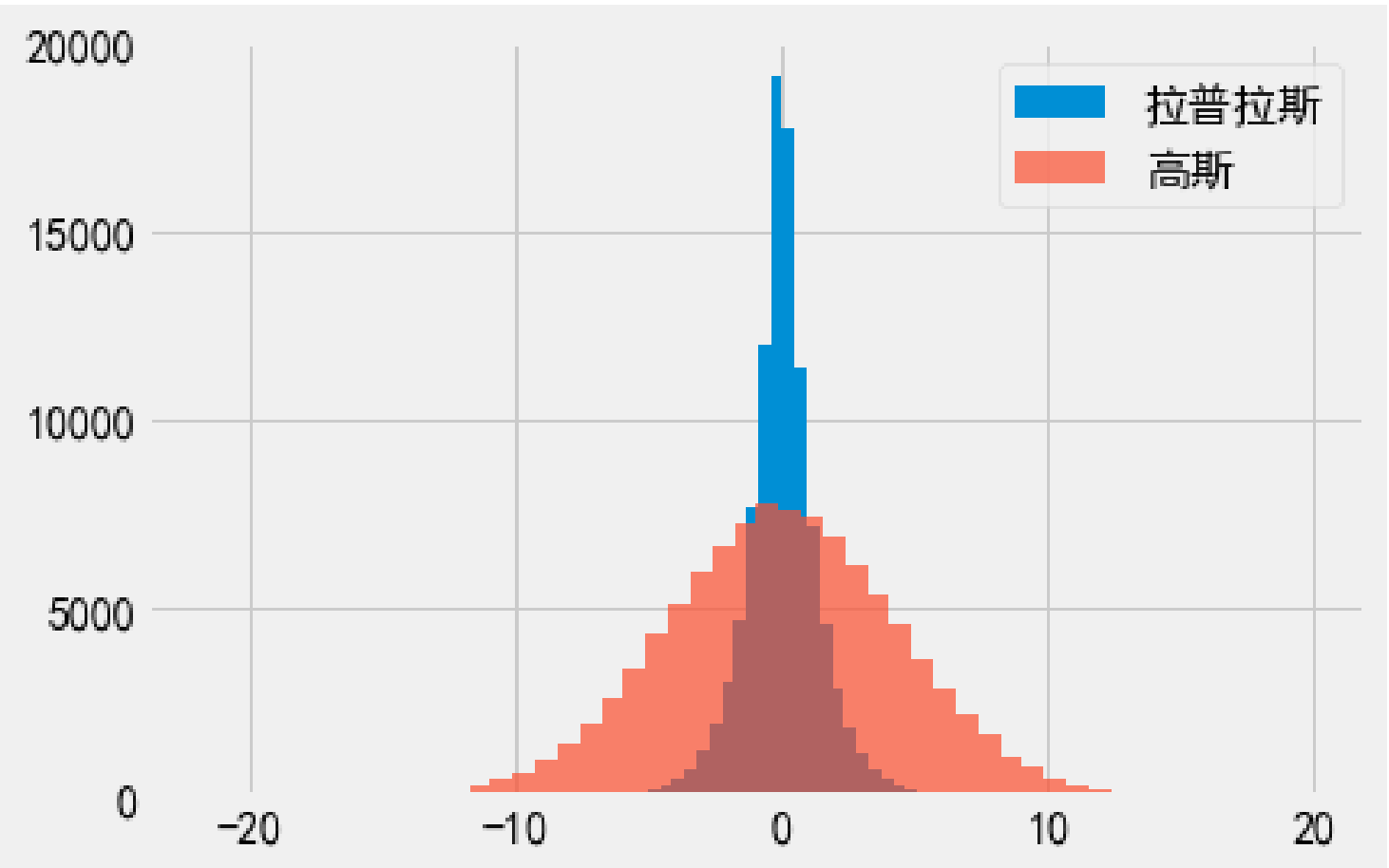
上图使用相同的 , 高斯机制的 .
高斯机制得到的输出相对较”平”, 相较于拉普拉斯机制, 更偏离真实值.
7.3 向量值函数及其敏感度
之前提到的函数均为将数据集映射到单一实数实值函数 .
拉普拉斯机制和高斯机制可扩展到向量值函数 .
实值函数的敏感度的定义是两个个体的差.
在向量值函数中, 敏感度就是两个向量的差所产生的新向量的标量长度.
??? 向量的长度就是向量的维度, 也就是个体包含的属性.
计算向量标量长度的方法: L1 范数 和 L2 范数.
7.3.1 L1 和 L2 范数
-
L1 范数 / 曼哈顿距离
向量各个元素的和.
-
L2 范数 / 欧式距离
向量各个元素平方和再求平方根.
L2 范数总是 L1 范数
7.3.2 L1 和 L2 敏感度
-
L1 敏感度
若 计算的到长度为 的敏感度向量, 每个元素的敏感度为 1. 通过 L1 范数计算, 的敏感度即为 .
-
L2 敏感度
若 计算的到长度为 的敏感度向量, 每个元素的敏感度为 1. 通过 L2 范数计算, 的敏感度即为 .
7.3.3 选择 L1 还是 L2
向量值拉普拉斯机制需要使用 L1 敏感度.
向量高斯机制既可使用 L1 敏感度, 也可以使用 L2 敏感度.
高斯机制的重要优势!
7.4 灾难机制
灾难机制 Catastrophe Mechanism
当 [0,1]中随机采样的数小于 差分隐私失败的概率 时, 返回真实值. 反之, 则输出带有噪声的结果.
import numpy as np
def catastrophe(x, sensitivity, epsilon, delta):
r = np.random.uniform(0, 1)
print("0,1中随机采样:",r)
if r < delta:
print(f"{r} < {delta}")
return x
else:
print(f"{r} > {delta}")
return x + np.random.laplace(0, sensitivity / epsilon)
x = 20
sensitity = 0.01
epsilon = 1
delta = 0.001
print("真实值:",x)
print("灾难机制输出:",catastrophe(x,sensitity,epsilon,delta))
⬇️ TODO ⬇️
还没搞懂…
7.5 高级组合性
k-折叠适应性组合 k-fold Adaptive Composition
7.6 近似差分隐私的高级组合性